7548. Счастливый турист
Как только
Счастливый Гарри въезжает в свой любимый кемпинг со всей семьей, он замечает
знак: "Палаточное размещение ограничено 5 днями в течение любого 8
дневного периода. Гарри только начинает свой 20 – дневный отдых. Каково максимальное
количество дней, когда Гарри может провести свой отпуск в лагере?
Сформулируем
задачу в более общем виде. Пусть l, p, v
(1 < l < p < v) – целые числа.
Палаточное размещение ограничено l
днями в течение любого p-дневного
периода. Счастливый Гарри начинает свой v-дневный
отдых. Какое наибольшее число дней своего отпуска Гарри сможет провести в
лагере?
Вход. Состоит из нескольких тестов. Каждый тест состоит из
одной строки, содержащей числа l, p и v.
Все числа являются 32-битовыми знаковыми целыми. Последняя строка содержит три
нуля и не обрабатывается.
Выход. Для каждого
теста вывести в одной строке его номер и количество дней, когда Счастливый
Гарри может разместиться в палатке во время своего отпуска. Следуйте формату,
приведенному в примере.
|
Пример
входа |
Пример
выхода |
|
5 8 20 5 8 17 0 0 0 |
Case 1: 14 Case 2: 11 |
РЕШЕНИЕ
математика
Анализ алгоритма
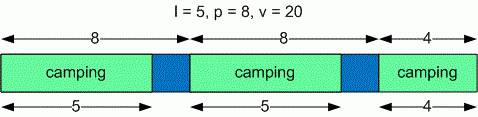
Полных p-дневных периодов во время v-дневного отдыха существует v / p.
Во время каждого p-дневного периода
Гарри может отдохнуть l дней. Кроме
полных p-дневных периодов у Гарри еще
остается на отдых v % p дней, которое может быть как меньше,
так и больше l дней. То есть кроме v / p
* l дней еще есть возможность
провести в кемпинге min(v % p, l)
дней.
Реализация алгоритма
Читаем входные данные. Вычисляем и выводим ответ.
cs = 1;
while(scanf("%d
%d %d",&l,&p,&v), l + p + v)
{
res = v / p * l + min(v % p, l);
printf("Case
%d: %d\n",cs++,res);
}